Większość funkcji posiada swoje przynajmniej lokalne wartości największe lub najmniejsze. Nie posiada ich np. funkcja liniowa oraz funkcje tangens i cotangens (ich wykresy uciekają do plus i minus nieskończoności.
Funkcja kwadratowa posiada zamiennie wartość największą albo najmniejszą (w zależności od kierunku ramion paraboli). Do jej wyznaczenia wystarczy użyć współrzędnych wierzchołka i własności współczynnika a. Te informacje znajdziesz tutaj.
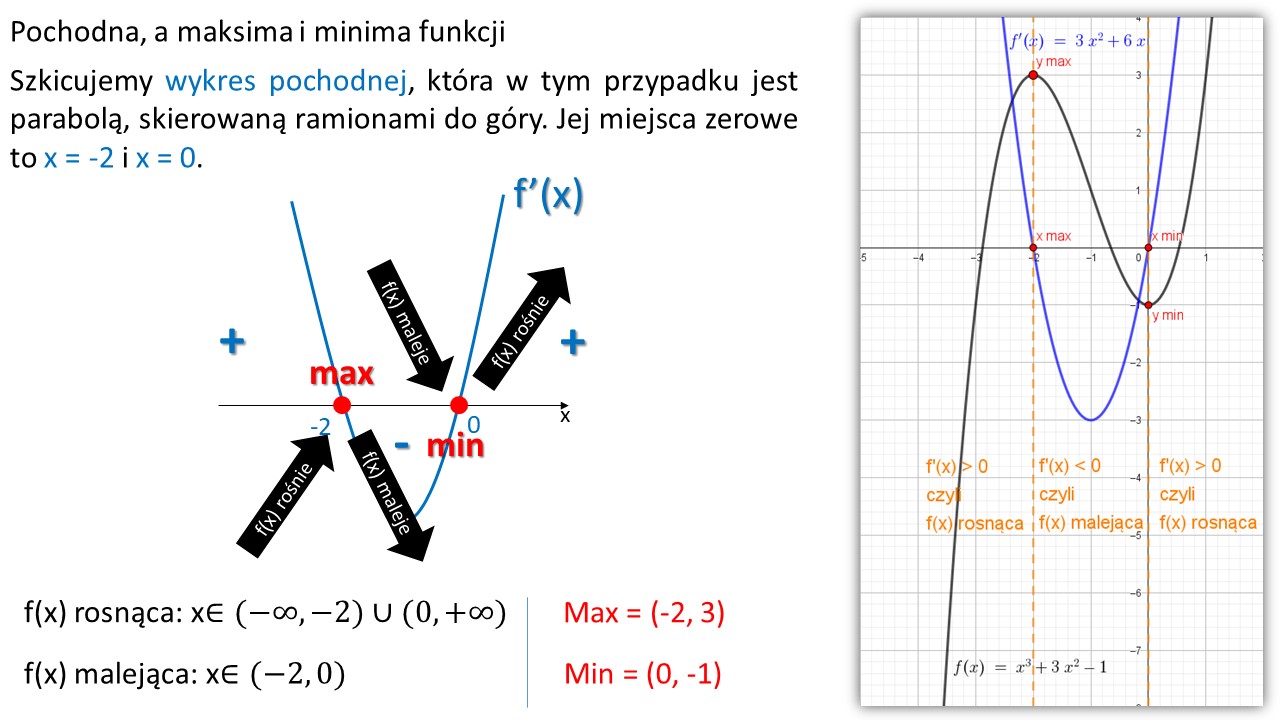
Funkcje wyższych stopni mogą nie posiadać wartości największej i najmniejszej w całej swojej dziedzinie, tak jak w przykładzie omawianym poniżej. Jednakże mogą posiadać maksima i minima lokalne, które dodatkowo dają możliwość zbadania monotoniczności funkcji.
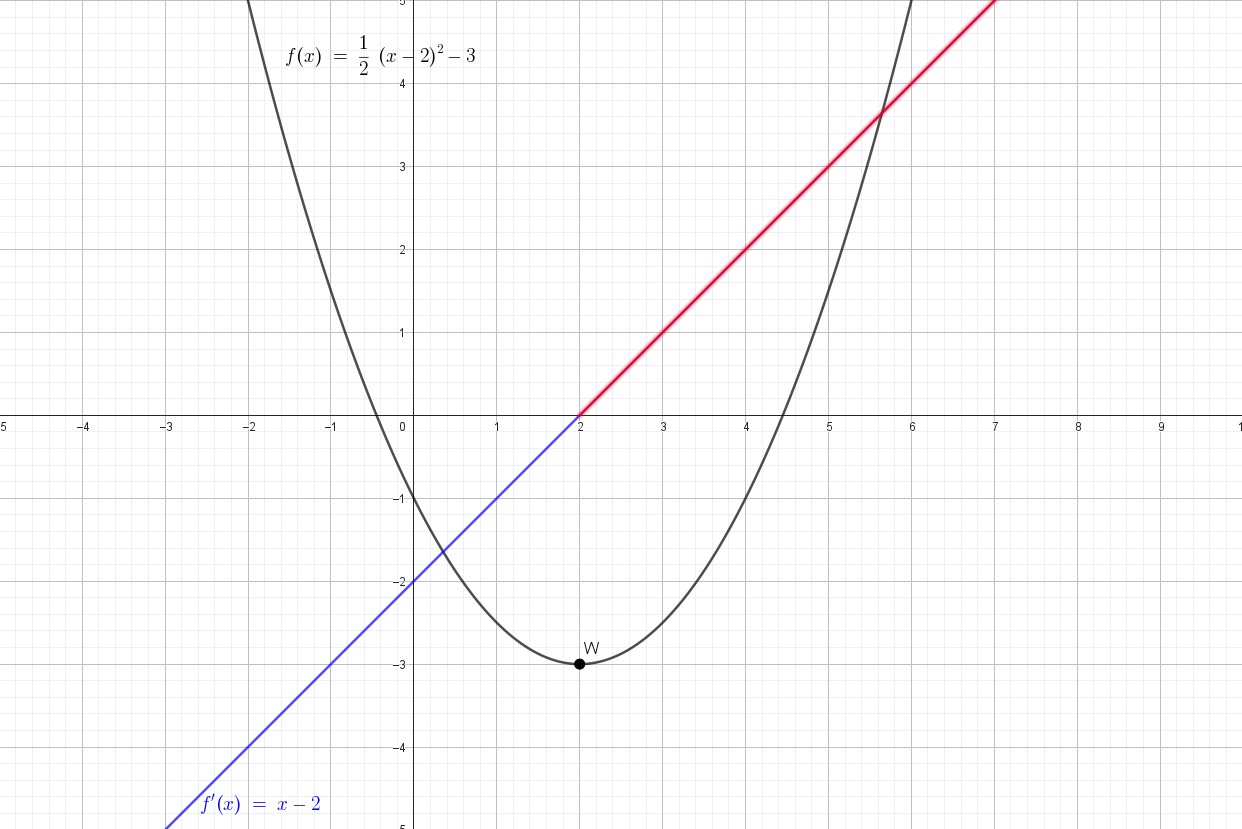
Najłatwiej jest to zauważyć na przykładzie funkcji kwadratowej (podanej w postaci kanonicznej). Miejsce zerowe pochodnej określa jej minimum (wierzchołek). Tam, gdzie pochodna jest dodatnia - funkcja rośnie, zaś gdy jest ujemna - maleje.